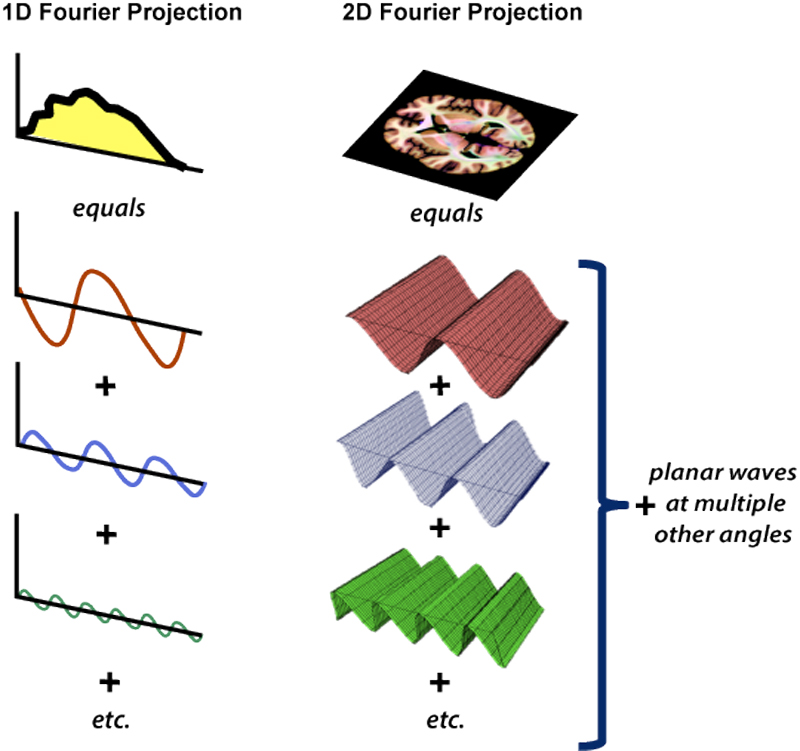
In a previous Q&A we introduced the Fourier series and Fourier transformation as a method to dissect out the frequency components of a 1-dimensional MR signal. The same idea can be extended into 2D, 3D and even higher dimensions.
|
The diagram to the right shows how a 2D brain image could be decomposed into planar waves of different amplitudes and frequencies. The sum of these many waves is used to build up a planar image.
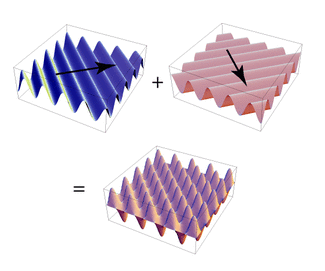
Unlike linear waves in one dimension, 2D planar waves may occur in any direction across the image (left-to-right, top-to-bottom, at 30°, 129°, etc.) Thus the Fourier summation must include all these angles and directions to represent the full image.
Individual planar waves are sometimes likened to lasagna noodles of varying sizes stacked at different angles to create the image.
|
Advanced Discussion (show/hide)»
No supplementary material yet. Check back soon!
References
Osgood B. N-dimensional Fourier Transform. Stanford Engineering Everywhere. Website with full course materials on the Fourier Transform.
Osgood B. N-dimensional Fourier Transform. Stanford Engineering Everywhere. Website with full course materials on the Fourier Transform.