|
Any periodically oscillating sinusoidal wave (or simple MR signal) has three fundamental properties: amplitude, frequency, and phase. These properties are explicitly apparent in the mathematical formulation for a sine wave:
S(t) = A sin(ωot − ϕ)
where S(t) is the signal as a function of time, A is the amplitude, ωo is the angular frequency, and ϕ is the instantaneous phase.
|
By adjusting these factors, the appearance of the sine wave can be varied. Instantaneous phase (ϕ) represents an angular shift between two sine waves and is measured in radians (or degrees). A sine wave and a cosine wave are 90° (π/2 radians) out of phase with each other.
After a period of time, Δt, two sine waves initially synchronized in phase but differing in frequency by Δω radians per second will develop a differential total phase shift (ΔΦ) given by: ΔΦ = Δω × Δt. Or in more general terms expressed by calculus:
After a period of time, Δt, two sine waves initially synchronized in phase but differing in frequency by Δω radians per second will develop a differential total phase shift (ΔΦ) given by: ΔΦ = Δω × Δt. Or in more general terms expressed by calculus:
|
Φ = ∫ ω(t) dt
where Φ is the total phase shift accumulated over a period of time (Δt) and ω(t) is the frequency shift that may vary as a function of time. The total accumulated phase shift (Φ) can be thought of as the area under a frequency vs time curve. This fact will prove useful when we discuss the phase changes induced by gradients or flow in later Q&A's.
|
If you still don't quite understand why (frequency x time) = phase, think about the units of measurement. Frequency is commonly measured in Hertz, or cycles per second. Time is measured in seconds. So frequency x time = (cycles/sec) x sec = # of cycles. Thus two sine waves differing in frequency by 200 Hz get progressively out of phase with each other by 200 cycles every second.
|
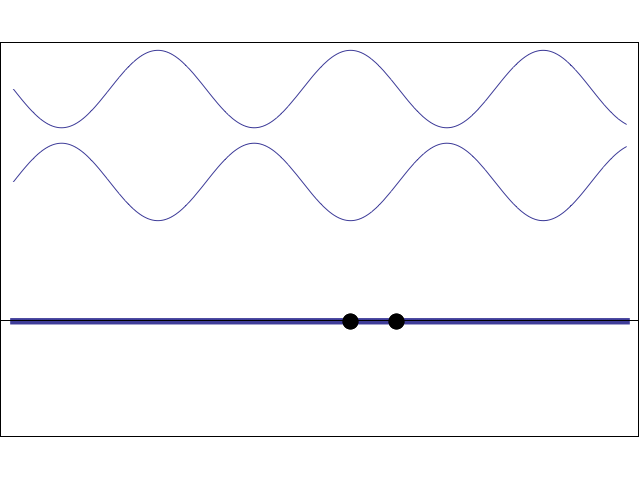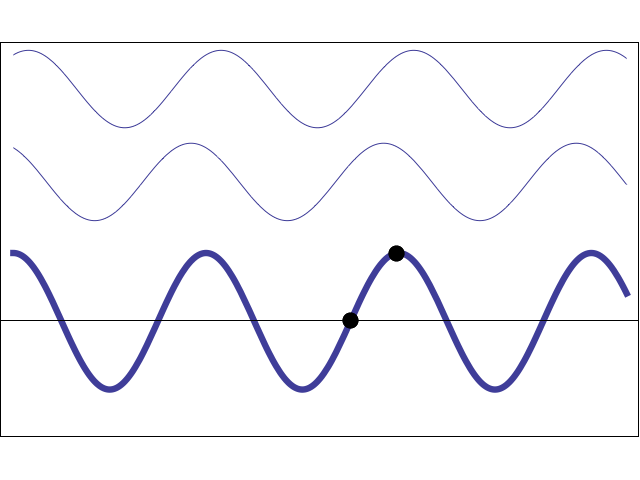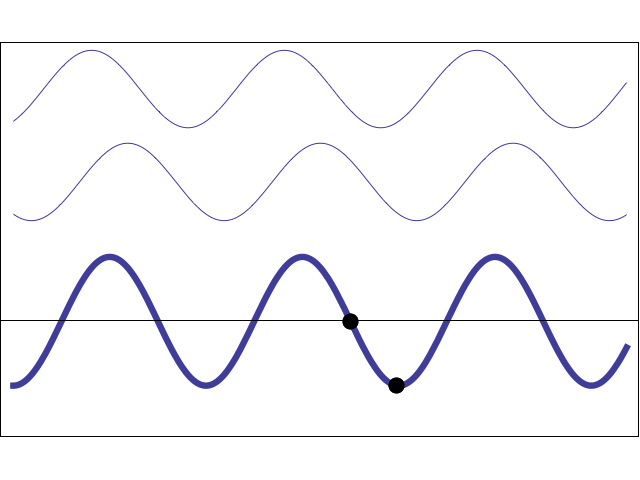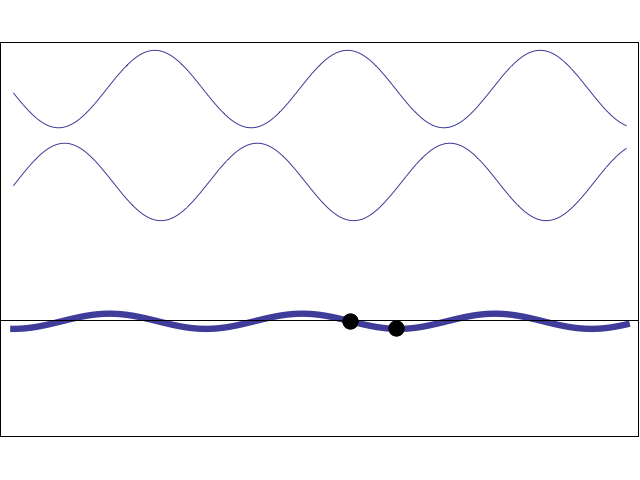
To understand the more complex aspects of frequency and phase encoding of the MR image, it is necessary to review what happens when two sine waves are added together. If two sine waves have the same frequency but different phases, their summation is another sine wave with the same base frequency but a different amplitude and phase. When the two waves are perfectly in phase with each other, their signals augment each other. When they are slightly out of phase with each other, the overall signal is diminished, and they are said to destructively interfere. When the phase shift between them reaches 180°, the two waves exactly cancel each other.
|
Advanced Discussion (show/hide)»
No supplementary material yet. Check back soon!
Related Questions
What is a gradient echo, and how does it differ from an FID?
What is a gradient echo, and how does it differ from an FID?