Prior to subjecting raw fMRI data to any type of statistical analysis, most of the following pre-processing steps are commonly performed.
 Montage view of source data from an fMRI series
Montage view of source data from an fMRI seriesallowing recognition and exclusion of aberrant individual slices
Quality Assurance: Inspection of source images. Individual slices in an fMRI acquisition commonly suffer from random variations in average signal intensity, noise spikes, ghosts, and data glitches. These may result from physiological sources (patient motion, respiration, cardiac pulsations, anxiety, drowsiness, drugs) or from the scanner itself (field inhomogeneities, eddy currents, gradient heating, electronics). If unrecognized and included in the data analysis, these may spoil the entire experiment. A quick visual review of all source images together in montage mode is highly recommended to search for and exclude ("scrub") aberrant slices that appear too bright, too dark, or contain artifacts. More sophisticated graphical and semi-automated methods to identify outlier data are also available.
|
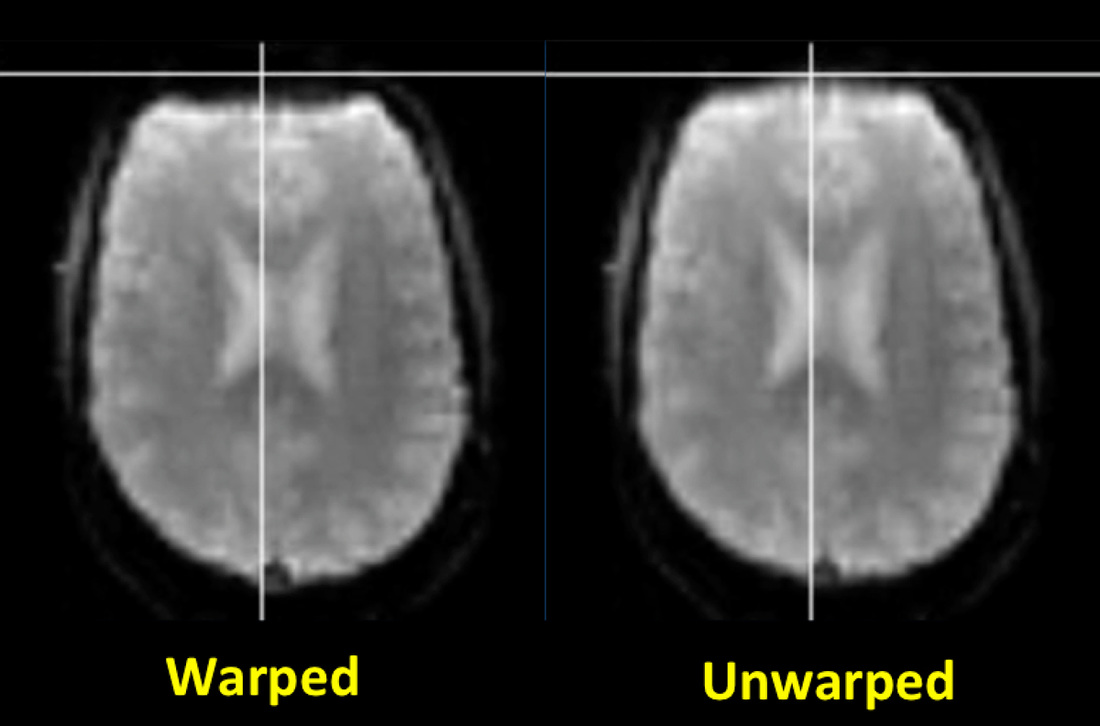
Distortion correction. Common fMRI/BOLD sequences acquire gradient echoes and hence are sensitive to magnetic inhomogeneity (T2*) effects. These cause spatial distortions and signal dropout especially near the skull base, typically affecting the anterior frontal and temporal lobes.
Field mapping and "unwarping" methods (described in the Advanced Discussion) are available to reduce these distortions. Although these techniques may be required for sophisticated neuropsychological experiments, they are not commonly used for basic eloquent cortex mapping in clinical fMRI studies. |
Slice timing correction. Most fMRI studies acquire one slice at a time, meaning that the signal recorded from one slice may be offset in time by up to several seconds when compared to another. The situation is even further complicated depending on whether the slices have been acquired in sequential (1,2,3,4,5,6...) or in interleaved (1,3,5,..2,4,6...) order and whether simultaneous multi-slice imaging has been employed. Although slice timing differences may not be important for simple block design experiments, they can impart considerable errors in rapid, event-related fMRI studies if not accounted for.

Two basic strategies have been developed for slice timing correction. Data shifting is the most commonly used method, where recorded points are moved to reflect their proper offset from the time of the stimulus. This method requires interpolation of points to fit the fixed, TR-based timing grid and thus produces some blurring and degradation of the data. An alternate (post-processing) strategy is model shifting, where the expected location of the hemodynamic response function (HRF) is varied, treating slice location as an additional independent variable in the subsequent statistical analysis. Sometimes temporal derivatives of the HRF are also incorporated in the model to improve accuracy.
 Residual mean-squared error
Residual mean-squared errorafter motion correction
Motion Correction. Head motion is the largest source of error in fMRI studies, and a variety of strategies have been developed to cope with this problem. Immobilization of the head using padding and straps is essential; even more rigid restrictions using bite bars and masks are occasionally employed. Proper coaching and training of the subject prior to imaging is important. Prospective motion correction using navigator echoes may be performed but more commonly motion correction is done retrospectively.
 Rotation and translation plots of the 6 parameters in a motion correction algorithm
Rotation and translation plots of the 6 parameters in a motion correction algorithmNote sudden head movement jump at acquisition #245. (Courtesy Chris Rorden)
The standard retrospective motion correction method considers the head as a rigid body with three directions of translation (displacement) and three axes of rotation. A single functional volume of a run is chosen as the reference to which runs in all other volumes are aligned. An iterative procedure is performed in which each volume is rotated and aligned with the reference, with the goal to minimize a cost function (such as the mean-squared difference). This iterative adjustment terminates once no further improvement can be achieved. All major fMRI analysis packages produce line plots allowing visual inspection of how translation and rotation parameters change from volume to volume (see figure above).

Temporal Filtering. fMRI data nearly always exhibit slow wandering of the baseline signal over time as well as rapid fluctuations due to noise. The removal of low frequency drifts is known as detrending. Detrending may be accomplished using either high-pass filtering after Fourier transformation or by time-domain averaging methods. Alternatively, gradual drifts can be removed later in the data analysis pipeline by adding a set of confound predictors (such as a discrete cosine transform basis set) to account for low-frequency fluctuations. High-frequency signal fluctuations (AKA "noise") can be removed by low-pass filtering. Low-pass filtering is generally not recommended for most studies, however, since it may distort estimation of individual HRFs and reduce the fMRI signals of interest.
 Spatial smoothing using Gaussian filters with various kernel widths
Spatial smoothing using Gaussian filters with various kernel widths(FWHM = full width half maximum)
Spatial Smoothing. Spatial smoothing is the averaging of signals from adjacent voxels. This improves the signal-to-noise ratio (SNR) but decreases spatial resolution, blurs the image, and smears activated areas into adjacent voxels. The process can be justified because closely neighboring brain voxels are usually inherently correlated in their function and blood supply. The standard method is to convolve ("multiply") the fMRI data with a 3D Gaussian kernel ("filter") that averages signals from neighboring voxels with weights that decrease with increasing distance from the target voxel. The optimal kernel size is disputed, depending on factors such as slice thickness and in-plane resolution and the need for spatial separation of small activation regions. In practice, the full width half maximum (FWHM) value of the Gaussian spatial filter is typically set to about 4-6 mm for single subject studies and to about 6-8 mm for multi-subject analyses.
Advanced Discussion (show/hide)»
Additional Comments About fMRI Pre-Processing
Quality Assurance
Although all slices should be quickly assessed visually, the initial slices of an fMRI acquisition should be especially scrutinized. This is the time when tissue magnetization may not have not yet reached a steady-state equilibrium and signal intensity may appear artificially high. Most scanners perform one or more “dummy scans” and discard the first 3-5 slices, but this is worth checking. For some experiments it may be desirable to censor even more initial slices (e.g., to allow a subject to acclimatize to loud scanner sounds). Graphical methods (illustrated below) permit rapid identification of outlier data. High-signal outliers result in false areas of activation; low-signal outliers create false areas of deactivation. Additional time series diagnostics include mean voxel intensity, variance of voxel intensity, and temporal signal-to-noise per slice.
An option called "Mean Intensity Adjustment" (or one with similar wording) is available in most fMRI software. Its purpose is to remove global fluctuations in average background signal from slice to slice. Before the current era of fully digital RF multi-transmit and receiver chains, this option was more widely used, but is now largely unnecessary for modern scanners operating at 3T or below. Intensity normalization may still be needed for fMRI studies at 7T or higher where RF-inhomogeneities can be more problematic.
Distortion Correction
Field mapping and unwarping. Basic rapid field mapping is commonly performed as a normal part of automated prescan procedures. In the simplest case a low-resolution dual echo sequence with relatively short TE's is first performed, with computation of magnitude and phase-difference images. The phase-difference images require unwrapping as all phase measurements (however large) are "wrapped" (compressed) over the range of 0°−360°. After phase unwrapping field map values are used to calculate corrective pixel shifts in the phase-encode direction, a process known as unwarping (not to be confused with unwrapping above!). Because field map artifacts and noise create problems, some spatial smoothing (often Gaussian) is typically performed as well as masking to exclude voxels outside of the brain. More sophisticated field mapping and unwarping techniques include those that continuously update during data acquisition.
Z-shimming. T2*-dephasing creates inhomogeneity in the z-(slice-select)-direction as well as in plane (xy-direction). To restore the signal a compensating gradient along the z-axis is applied to be sure the k-space trajectory returns to the origin at time TE. As commonly implemented, images are collected using 3-4 different positive and negative z-gradients applied immediately after the RF-pulse and then combined using a square root sum of squares approach. The method may also be applied to reduce in-plane artifacts in the phase-encode direction, and a 3D-implementation has also been developed. A major disadvantage of z-shimming is the time penalty, meaning a longer TR with fewer slices and decreased temporal resolution. Additionally, portions of the original image not suffering from susceptibility-induced signal loss can be dephased by the z-shimming gradients and potentially made worse.
It should be noted that distortion correction techniques such as field mapping, unwarping, and z-shimming cannot restore fMRI signals lost due to dephasing. These techniques merely attempt to reassign recorded signals to the proper points in space from which they arose.
Slice-Timing Correction
Interpolation of the time-shifted data points may be performed by nearest neighbor, tri-linear, multipoint spline, or sinc approximations. Nearest neighbor and linear interpolation are the fastest, but introduce more smoothing artifacts; cubic/multipoint B-spline or (Hanning-windowed) sinc methods are generally preferred. These latter techniques tend to spread the artifact out over a wider range of nearby voxels. Whether to do slice time-correction as a pre-processing step vs post-processing HRF model shifting remains in dispute. Likewise, if the pre-processing option is chosen, whether to do slice-timing correction before or after motion correction is also not agreed upon, and may depend on the expected degree of motion as well as slice order.
Motion Correction
The iterative minimization procedure used for fMRI motion correction schemes is typically a nonlinear least squares routine (e.g., Levenberg-Marquardt). Possible errors in this process may result from finding only a local (rather than global) minimum of the cost function, leading to suboptimal results. Once motion parameters for realignment have been determined, they are applied to create a new 3D motion-corrected data set. Creation of the corrected data set requires spatial interpolation, as the new data points typically fall in between the original uncorrected data points. This process may be computationally-intensive, so usually some combination of (fast) linear interpolation is used during the initial motion correction steps, followed by a more time-consuming interpolation method (such as windowed sinc) for the final spatial transformation.
Typically head motions are relatively small (<2 mm) during normal fMRI experiments, so the assumptions underlying this rigid body approach are justified. However, sudden abrupt head motion (as seen near volume 245 in the figure above) will violate these conditions and may not produce an appropriate correction for motion.
Rigid body transformations cannot compensate for non-linear effects. These include field inhomogeneity effects, motion during slice acquisition, interpolation artifacts, and spin-excitation history effects. Field inhomogeneity effects may be the most important. Even though rigid head motion can be corrected in image space, head displacements affect magnetic field homogeneity and shimming, so even with perfect realignment some motion-related errors persist. These additional sources of residual motion error are often referred to as the residual variance and may be addressed in part by unwarping (described above).
Typically head motions are relatively small (<2 mm) during normal fMRI experiments, so the assumptions underlying this rigid body approach are justified. However, sudden abrupt head motion (as seen near volume 245 in the figure above) will violate these conditions and may not produce an appropriate correction for motion.
Rigid body transformations cannot compensate for non-linear effects. These include field inhomogeneity effects, motion during slice acquisition, interpolation artifacts, and spin-excitation history effects. Field inhomogeneity effects may be the most important. Even though rigid head motion can be corrected in image space, head displacements affect magnetic field homogeneity and shimming, so even with perfect realignment some motion-related errors persist. These additional sources of residual motion error are often referred to as the residual variance and may be addressed in part by unwarping (described above).
Temporal Filtering
Low frequency drifts in fMRI data are very common, and if not accounted for, will severely reduce the power of the statistical analysis. They will also invalidate event-related averaging, which assumes a stationary level of signal over the course of an experiment. Accordingly, removing these drifts is a mandated step for every fMRI study. This must be done carefully, however, as true condition-related signal changes may be inadvertently removed by this process if improperly applied.
Typically, low frequency drifts are removed as part of the preprocessing pipeline. They may also be removed during the post-processing/statistical analysis phase by incorporating them as “nuisance predictors” in the General Linear Model (GLM). Both approaches are commonly used (although not together) with generally similar results.
If the pre-processing route is chosen, then a Fourier frequency filtering method is typically employed. Here, the fMRI signal time course for a voxel is transformed into the frequency domain using a Fast Fourier Transform (FFT). A certain group of low frequencies (say 1-3 cycles) is removed, and the filtered data retransformed back into the time domain.
Typically, low frequency drifts are removed as part of the preprocessing pipeline. They may also be removed during the post-processing/statistical analysis phase by incorporating them as “nuisance predictors” in the General Linear Model (GLM). Both approaches are commonly used (although not together) with generally similar results.
If the pre-processing route is chosen, then a Fourier frequency filtering method is typically employed. Here, the fMRI signal time course for a voxel is transformed into the frequency domain using a Fast Fourier Transform (FFT). A certain group of low frequencies (say 1-3 cycles) is removed, and the filtered data retransformed back into the time domain.
|
Because FFT frequency filtering does not work well with purely linear trends, several fMRI software packages first remove linear trends in the time domain with a simple regression tool before transforming into the frequency domain. Additionally Fourier-based filtering techniques may also introduce spurious autocorrelations into the data.
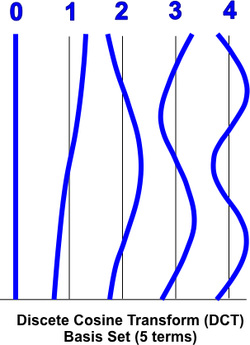
Accounting for low frequency drifts can also be done as a post-processing step, including them as confound predictors in the GLM. Some investigators prefer this approach. In brief, 3-5 additional columns are added to the GLM design matrix (X) composed of low-frequency waves. These may be a low frequency Fourier basis set of sines and cosines plus a constant linear trend term or a slightly more sophisticated (but closely related) discrete cosine transform (DCT) set. |
References
Ashburner J, Friston KJ. Rigid body registration. In: Frackowiak RSJ (ed). Human Brain Function, 2nd ed. London: Academic Press, 2004. (pdf made available on-line by the authors at http://www.fil.ion.ucl.ac.uk/spm/doc/books/hbf2/)
Berman H, Mulders J, Goebel R. Anatabacus v1.1: Calculator for image distortions for Brain Voyager QX, 2014. (Detailed manual describing procedures for distortion correction using Brain Voyager, available from this link. Includes useful information about how to compute field maps and other practical measures for reducing susceptibility distortions.)
Chen JE, Glover GH. Functional magnetic imaging methods. Neuropsychol Rev 2015; 25:289-313.
Friston KJ, Josephs O, Zarahn E, et al. To smooth or not to smooth? Bias and efficiency in fMRI time-series analysis. NeuroImage 2000; 12: 196-208. (discussion of temporal smoothing, including bandpass filtering and whitening).
Maclaren J, Herbst M, Speck O, Zaitsev M. Prospective motion correction in brain imaging: a review. Magn Reson Med 2013; 69: 621–636.
Mikl M, Maraček R, Hluštík P, et al. Effects of spatial smoothing on fMRI group inferences. Magn Reson Imaging 2008; 26:490-503.
Sladky R, Friston KJ, Tröstl J, et al. Slice-timing effects and their correction in functional MRI. Neuroimage 2011; 58:588-594.
Tanabe J Miller D, Tregellas J, et al. Comparison of detrending methods for optimal fMRI preprocessing. NeuroImage 2002; 15:902–907.
The FIL Methods Group. SPM12 Manual. Welcome Trust Center for Neuroimaging, London, 2016. (describes preprocessing steps available in the SPM program).
Ashburner J, Friston KJ. Rigid body registration. In: Frackowiak RSJ (ed). Human Brain Function, 2nd ed. London: Academic Press, 2004. (pdf made available on-line by the authors at http://www.fil.ion.ucl.ac.uk/spm/doc/books/hbf2/)
Berman H, Mulders J, Goebel R. Anatabacus v1.1: Calculator for image distortions for Brain Voyager QX, 2014. (Detailed manual describing procedures for distortion correction using Brain Voyager, available from this link. Includes useful information about how to compute field maps and other practical measures for reducing susceptibility distortions.)
Chen JE, Glover GH. Functional magnetic imaging methods. Neuropsychol Rev 2015; 25:289-313.
Friston KJ, Josephs O, Zarahn E, et al. To smooth or not to smooth? Bias and efficiency in fMRI time-series analysis. NeuroImage 2000; 12: 196-208. (discussion of temporal smoothing, including bandpass filtering and whitening).
Maclaren J, Herbst M, Speck O, Zaitsev M. Prospective motion correction in brain imaging: a review. Magn Reson Med 2013; 69: 621–636.
Mikl M, Maraček R, Hluštík P, et al. Effects of spatial smoothing on fMRI group inferences. Magn Reson Imaging 2008; 26:490-503.
Sladky R, Friston KJ, Tröstl J, et al. Slice-timing effects and their correction in functional MRI. Neuroimage 2011; 58:588-594.
Tanabe J Miller D, Tregellas J, et al. Comparison of detrending methods for optimal fMRI preprocessing. NeuroImage 2002; 15:902–907.
The FIL Methods Group. SPM12 Manual. Welcome Trust Center for Neuroimaging, London, 2016. (describes preprocessing steps available in the SPM program).
Related Questions
How is fMRI data processed and analyzed?
How is fMRI data processed and analyzed?