The diffusion tensor was briefly discussed in a previous Q&A where the concept of diffusion anisotropy was introduced. Biological tissues are highly anisotropic, meaning that their diffusion rates are not the same in every direction. For routine DW imaging we often ignore this complexity and reduce diffusion to a single average value, the apparent diffusion coefficient (ADC), but this is overly simplistic.

Diffusion Tensor
A superior method to model diffusion in complex materials is to use the diffusion tensor, a [3 x 3] array of numbers corresponding to diffusion rates in each combination of directions. The three diagonal elements (Dxx, Dyy, Dzz) represent diffusion coefficients measured along each of the principal (x-, y- and z-) laboratory axes. The six off-diagonal terms (Dxy, Dyz, etc) reflect reflect the correlation of random motions between each pair of principal directions.
For anisotropic diffusion, however, the diagonal elements are unequal and the off-diagonal elements cannot be ignored. An additional complicating factor is that the value of each tensor element depends upon the frame of reference in which it is measured.
To measure these individual tensor elements we typically begin in the so-called laboratory (x-y-z) frame, which for clinical MRI is typically aligned with the patient's body and main magnetic field. Gradients are applied in different directions and several sets of raw data (source) images are obtained. After some filtering and other mathematical corrections, linear regression techniques are applied to the data to create estimates for each tensor component. Because x→y and y→x diffusivities should be the same, mirror-image off-diagonal elements are equal (Dxy = Dyx, Dyz = Dzy, and Dxz = Dzx). This means the diffusion tensor matrix is symmetric with only 6 unique elements. To estimate all of them we need a minimum of 7 measurements: one baseline (b0) and 6 source data sets.
To measure these individual tensor elements we typically begin in the so-called laboratory (x-y-z) frame, which for clinical MRI is typically aligned with the patient's body and main magnetic field. Gradients are applied in different directions and several sets of raw data (source) images are obtained. After some filtering and other mathematical corrections, linear regression techniques are applied to the data to create estimates for each tensor component. Because x→y and y→x diffusivities should be the same, mirror-image off-diagonal elements are equal (Dxy = Dyx, Dyz = Dzy, and Dxz = Dzx). This means the diffusion tensor matrix is symmetric with only 6 unique elements. To estimate all of them we need a minimum of 7 measurements: one baseline (b0) and 6 source data sets.
The values we calculate for each tensor component (such as Dxx or Dxy), however, are not unique, being dependent on the (x-y-z) frame of reference chosen for measurement. Had we selected a different coordinate system (x'-y'-z') not aligned with the patient but at some arbitrary angle, the calculated values (Dx'x' or Dx'y') would have been completely different.
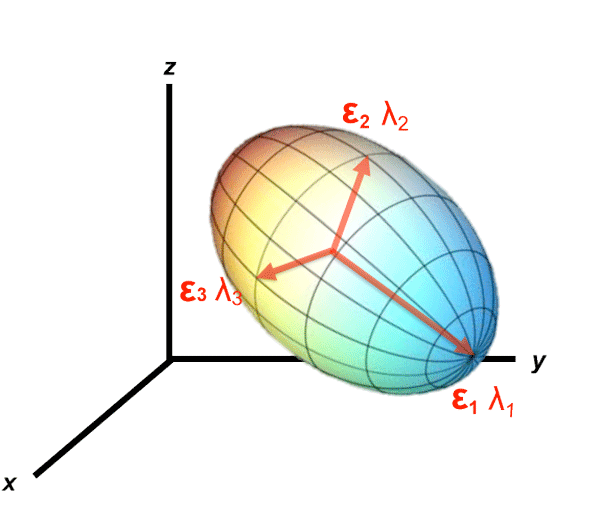
Fortunately an ideal frame of reference for viewing the diffusion tensor exists and can be determined using measurements obtained from any frame of reference. This optimal coordinate system is based upon the diffusion ellipsoid, whose main axis is parallel to the principal diffusion direction within a voxel. This principal axis often corresponds to anatomic features such as white matter tracts or fascial planes.
The major and minor axes of the diffusion ellipsoid are defined by thee orthogonal unit vectors (ε1, ε2, and ε3) known as eigenvectors. The length of each eigenvector (εi) is multiplied by a factor λi, called the eigenvalue. The eigenvalues of the ellipsoid are proportional to Einstein's root mean squared diffusion displacement in each direction. By convention, eigenvalues are labeled in descending order of magnitude (λ1 ≥ λ2 ≥ λ3).
Fortunately an ideal frame of reference for viewing the diffusion tensor exists and can be determined using measurements obtained from any frame of reference. This optimal coordinate system is based upon the diffusion ellipsoid, whose main axis is parallel to the principal diffusion direction within a voxel. This principal axis often corresponds to anatomic features such as white matter tracts or fascial planes.
The major and minor axes of the diffusion ellipsoid are defined by thee orthogonal unit vectors (ε1, ε2, and ε3) known as eigenvectors. The length of each eigenvector (εi) is multiplied by a factor λi, called the eigenvalue. The eigenvalues of the ellipsoid are proportional to Einstein's root mean squared diffusion displacement in each direction. By convention, eigenvalues are labeled in descending order of magnitude (λ1 ≥ λ2 ≥ λ3).
|
An additional benefit to using the diffusion ellipsoid is that in this frame of reference, the off-diagonal elements disappear. The set of eigenvalues define a matrix with only 3 diagonal elements denoted by the symbol Λ ("capital lambda") that appears in many advanced treatises about diffusion tensors.
|
Advanced Discussion (show/hide)»
No supplementary material yet. Check back soon!
References
Nucifora PGP, Verma R, Lee S-K, Melhem ER. Diffusion-tensor MR imaging and tractography: exploring brain microstructure and connectivity. Radiology 2007; 245: 367-384. [review]
Shimony JS, McKinstry RC, Akbudak E, et al. Quantitative diffusion-tensor anisotropy brain MR imaging: normative human data and anatomic analysis. Radiology 1999; 212:770-784.
Hermoye L, Wakana S, Laurent J-P, et al. White matter atlas. Accessed at www.dtiatlas.org. (Cool site with a DTI-based whole-brain atlas. You select at tract by name and it shows it to you in multiple color images).
Jellison BJ, Field AS, Medow J, et al. Diffusion tensor imaging of cerebral white matter: a pictorial review of physics, fiber tract anatomy, and tumor imaging patterns. AJNR Am J Neuroradiol 2004; 25:356-369.
Mukherjee P, Berman JI, Chung SW, et al. Diffusion tensor MR imaging and fiber tractography: theoretic underpinnings. AJNR Am J Neuroradiol 2008; 29:632-640. (A two-part series, very nice).
Mukherjee P, Chung SW, Berman JI, et al. Diffusion tensor MR imaging and fiber tractography: technical considerations. AJNR Am J Neuroradiol 2008; 29:843-52.
Nucifora PGP, Verma R, Lee S-K, Melhem ER. Diffusion-tensor MR imaging and tractography: exploring brain microstructure and connectivity. Radiology 2007; 245: 367-384. [review]
Shimony JS, McKinstry RC, Akbudak E, et al. Quantitative diffusion-tensor anisotropy brain MR imaging: normative human data and anatomic analysis. Radiology 1999; 212:770-784.
Hermoye L, Wakana S, Laurent J-P, et al. White matter atlas. Accessed at www.dtiatlas.org. (Cool site with a DTI-based whole-brain atlas. You select at tract by name and it shows it to you in multiple color images).
Jellison BJ, Field AS, Medow J, et al. Diffusion tensor imaging of cerebral white matter: a pictorial review of physics, fiber tract anatomy, and tumor imaging patterns. AJNR Am J Neuroradiol 2004; 25:356-369.
Mukherjee P, Berman JI, Chung SW, et al. Diffusion tensor MR imaging and fiber tractography: theoretic underpinnings. AJNR Am J Neuroradiol 2008; 29:632-640. (A two-part series, very nice).
Mukherjee P, Chung SW, Berman JI, et al. Diffusion tensor MR imaging and fiber tractography: technical considerations. AJNR Am J Neuroradiol 2008; 29:843-52.
Related Questions
How do you make a DW image?
How do you make a DW image?