|
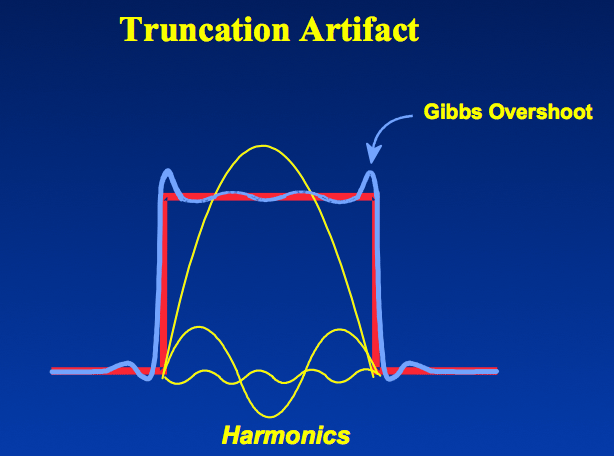
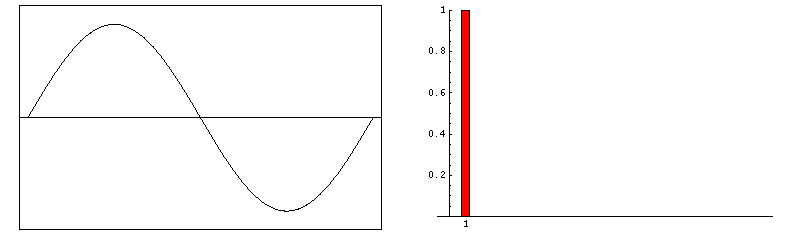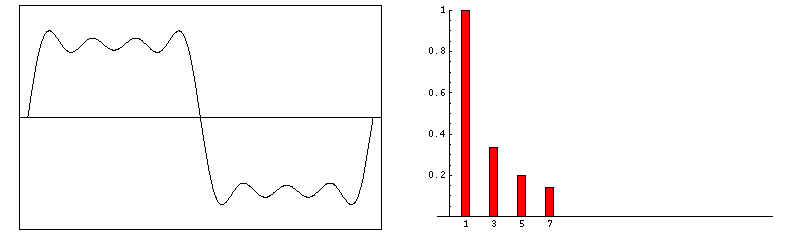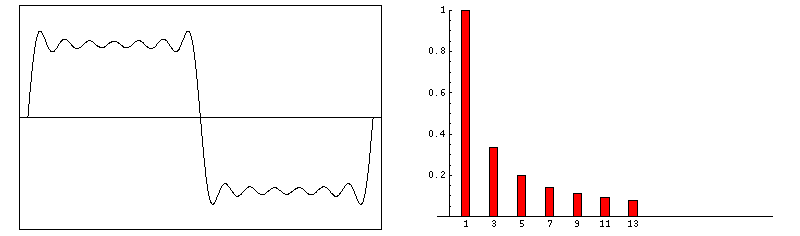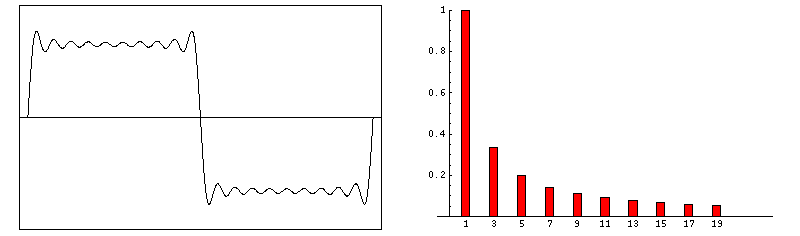
Gibbs artifacts occur as a consequence of using Fourier transforms to reconstruct MR signals into images. In theory, any signal can be represented as an infinite summation of sine waves of different amplitudes, phases, and frequencies. In MR imaging, however, we are restricted to sampling a finite number of frequencies and must therefore approximate the image by using only a relatively few harmonics in its Fourier representation. The Fourier series, then, is cut short or truncated, hence the name for this artifact.
|
|
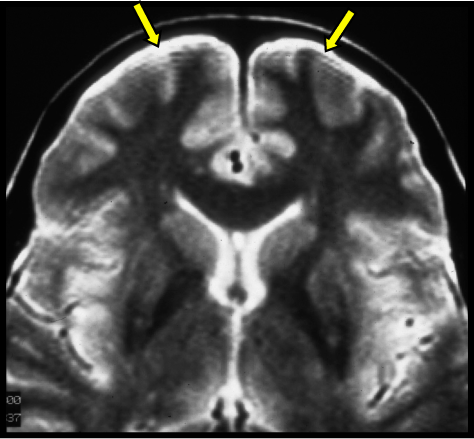
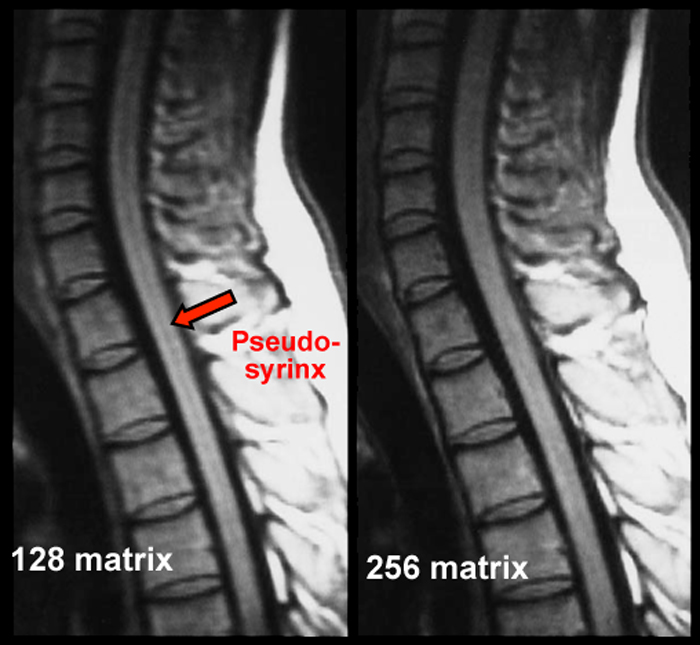
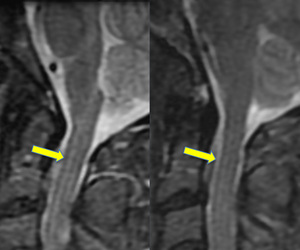
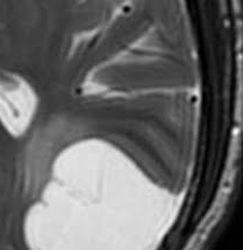
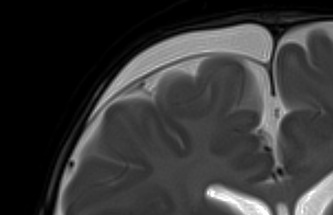
If the signal intensity of an object changes gradually in space, only a few Fourier terms are needed, and truncation errors are not evident. At high-contrast interfaces, however, truncation of the Fourier series results in significant artifacts, manifested by variable undershoot and overshoot oscillations. Depending upon the number of pixels spanning a high-contrast interface, truncation artifacts may have a variety of forms, including artifactual false widening of the edges at these interfaces, or edge enhancement of the interface and distortion of tissues immediately adjacent to the interface. For example, the high signal in the center and dark edges of the spinal cord (left) is another manifestation of the truncation artifact.
|
Advanced Discussion (show/hide)»
Additional Notes on the Gibbs Artifact and Phenomenon
The Gibbs (truncation) artifact is named after 19th Century mathematical physicist Josiah W. Gibbs. (Note that if an apostrophe is used it must be placed after the "s", not before it -- Gibbs', not Gibb's!)
Amongst his many other contributions to science (including Gibbs free energy in thermodynamics and the vector dot- and cross-product notations in math), Gibbs studied how Fourier series behaved at discontinuities. He described the overshoot and ripples arising at sharp edges which we now appreciate as truncation artifacts on MR images.
An interesting mathematical feature of the Gibbs phenomenon is that even with an infinite number of terms, the ripples will disappear but a remaining 8.9% overshoot will forever exist at the discontinuities. This unusual feature occurs because the Fourier series is point-wise, but not uniformly convergent.
Zero-filling (ZIP) methods, commonly used in MRI, are responsible for truncation artifacts. Sampling low frequencies in k-space is equivalent to using a rectangular sampling window in the frequency domain. The image produced by zero filling is equivalent to the convolution of the original image with a sinc function. (The sinc function, you may recall, is the inverse Fourier transform of a rectangular window). If the rectangular window were replaced by a smoothly decreasing (e.g. Hamming) window, truncation artifacts can be reduced.
Block KT, Uecker M, Frahm J. Suppression of MRI truncation artifacts using total variation constrained data extrapolation. Int J Biomed Imaging 2008; Article ID 184123:1-8.
Gibbs, JW. Fourier’s series. Nature 1899; 1539(59):606. (Gibbs’ letter to Nature, correcting his original article of 1898, and in which he describes the overshoot at the limits of a Fourier series.)
Levy LM, Di Chiro G, Brooks RA, et al. Spinal cord artifacts from truncation errors during MR imaging. Radiology 1988; 166:479-483.
Czervionke LF, Czervionke JM, Daniels DL, Haughton VM. Characteristic features of MR truncation artifacts. AJR Am J Roentgenol 1988; 151:1219-1228.
What is a Fourier transform?
What produces the dark-rim artifact on cardiac perfusion MRI?