It is indeed true that 90°and 180° pulses do not have to be used to generate a spin echo. In fact, pulses with any flip angles can be used. In his original description of spin echoes, Hahn employed a 90°-90° pair of RF-pulses. When pulses other than 90°-180° are used, the resultant spin echo is sometimes differentiated by calling it a Hahn echo (though many authors consider all echoes to be Hahn echoes).
The reason 90°-180° pairs are most commonly used is that this combination produces the maximum possible echo signal. The maximum SE intensity of a 90°-90° pair is only half as large as that produced by a 90°-180° pair. In general, if the first RF-pulse has flip angle α1 and the second has flip angle α2, the maximum signal intensity of the Hahn echo will be smaller than the conventional (90°-180°) echo by a factor of (sin α1)•(sin² α2/2).
The reason 90°-180° pairs are most commonly used is that this combination produces the maximum possible echo signal. The maximum SE intensity of a 90°-90° pair is only half as large as that produced by a 90°-180° pair. In general, if the first RF-pulse has flip angle α1 and the second has flip angle α2, the maximum signal intensity of the Hahn echo will be smaller than the conventional (90°-180°) echo by a factor of (sin α1)•(sin² α2/2).
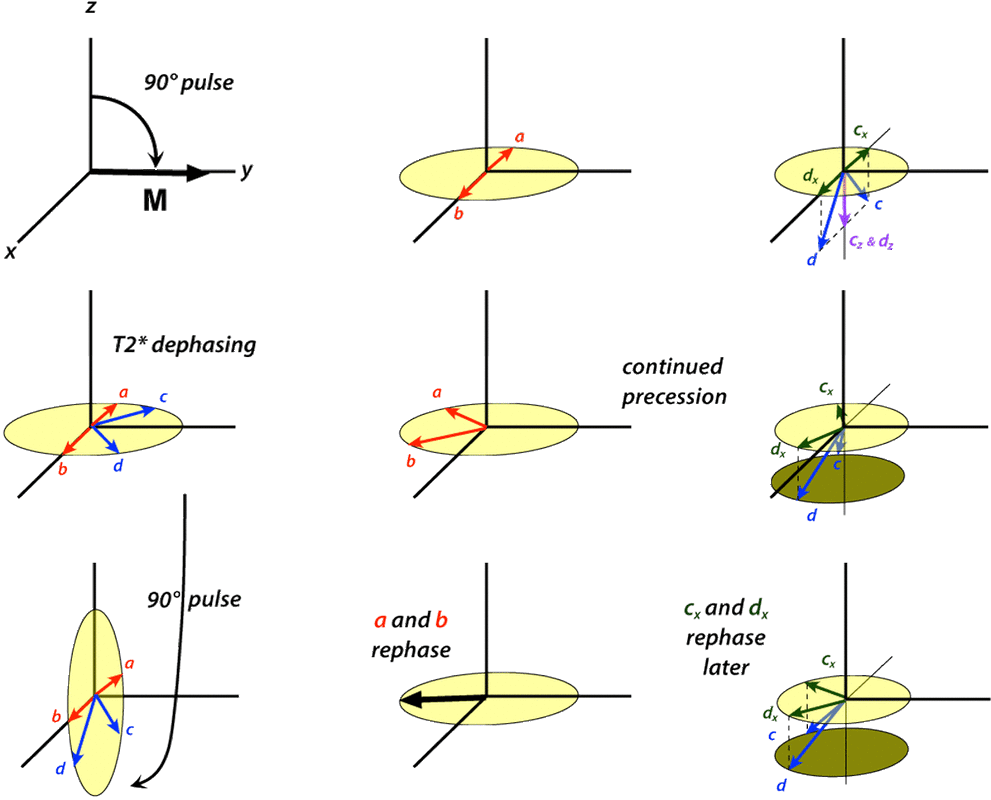
The diagram to the below provides an introduction as to some of the interesting phenomena occurring during a 90°-90°-echo sequence.
The first two drawings in the left column show the expected effect of the initial 90°-pulse and T2*-dephasing. For illustrative purposes we have selected four spins (a,b,c, and d) that have slightly dephased due to local field inhomogeneities. Spins a and c are in local fields lower than Bo, are precessing slightly slower than the Larmor frequency, and are losing phase. Spins b and d are in local fields higher than Bo, precessing faster, and gaining phase. Moreover, we have picked the spin pairs (a-b) and (c-d) to have local field offsets of the same magnitude but opposite polarities, so they gain or lose phase relative to their partner at the same relative rates.
The third drawing (bottom left) shows the effect of the second 90°-pulse. We will first focus our attention on spins a and b which, by chance, have just reached the −x and +x axes at the time of the second 90°-pulse. By virtue of their unique positions along the ±x axes, these spins will not be affected by the second 90°-pulse. They will continue precessing in the transverse plane and at the expected time (TE = 2 x the interpulse delay) will completely rephase and form a tiny echo along the −y axis.
The first two drawings in the left column show the expected effect of the initial 90°-pulse and T2*-dephasing. For illustrative purposes we have selected four spins (a,b,c, and d) that have slightly dephased due to local field inhomogeneities. Spins a and c are in local fields lower than Bo, are precessing slightly slower than the Larmor frequency, and are losing phase. Spins b and d are in local fields higher than Bo, precessing faster, and gaining phase. Moreover, we have picked the spin pairs (a-b) and (c-d) to have local field offsets of the same magnitude but opposite polarities, so they gain or lose phase relative to their partner at the same relative rates.
The third drawing (bottom left) shows the effect of the second 90°-pulse. We will first focus our attention on spins a and b which, by chance, have just reached the −x and +x axes at the time of the second 90°-pulse. By virtue of their unique positions along the ±x axes, these spins will not be affected by the second 90°-pulse. They will continue precessing in the transverse plane and at the expected time (TE = 2 x the interpulse delay) will completely rephase and form a tiny echo along the −y axis.
But what about spins c and d that were lagging a and b and didn't make it all the way to the ±x axes at the time of the second 90°-pulse? In fact, nearly all of the spins in the sample will be more like c and d (rather than the special case of a and b lying along the x-axes).
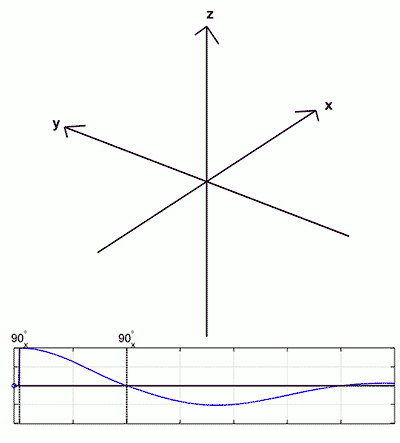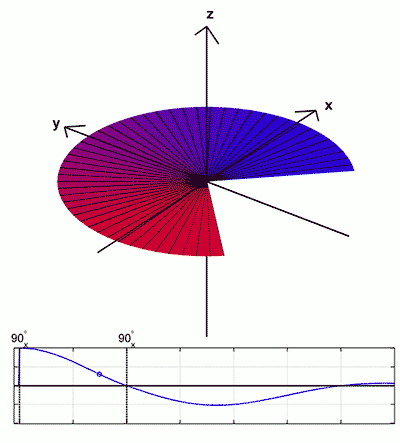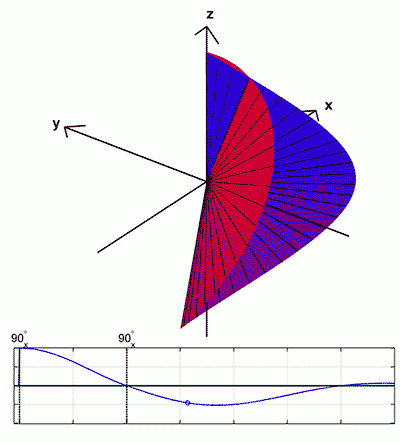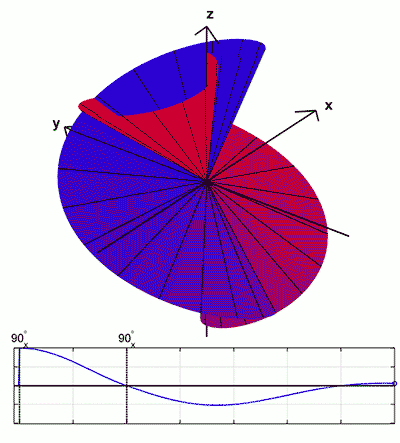
After the second 90°-pulse, spins c and d now lie in the vertical (xz-) plane. Each can be considered to have independent vector components along the x- and z-axes respectively that will be denoted by cx, cz, dx, and dz. Note that each component will be smaller than c and d though their vector sum will be of the same magnitude.
At the time of the second 90°-pulse the x-components (cx and dx) are aligned along the ±x axes, just like a and b. Over time cx and dx will continue to precess in the horizontal (xy-) plane and eventually rephase. But because they are precessing more slowly than a and b this rephasing will occur at a time later than the time when a and b rephase. The magnitude of the cx-dx "mini-echo" will also be smaller than the a-b mini-echo, because cx and dx are smaller than a and b.
After the second 90°-pulse, spins c and d now lie in the vertical (xz-) plane. Each can be considered to have independent vector components along the x- and z-axes respectively that will be denoted by cx, cz, dx, and dz. Note that each component will be smaller than c and d though their vector sum will be of the same magnitude.
At the time of the second 90°-pulse the x-components (cx and dx) are aligned along the ±x axes, just like a and b. Over time cx and dx will continue to precess in the horizontal (xy-) plane and eventually rephase. But because they are precessing more slowly than a and b this rephasing will occur at a time later than the time when a and b rephase. The magnitude of the cx-dx "mini-echo" will also be smaller than the a-b mini-echo, because cx and dx are smaller than a and b.
Because most paired spins (like c and d) are precesing in planes parallel to the main (xy-plane) after the second 90°-pulse and come back into phase at sligtly different times depending on their phase shifts, Hahn referred to this refocusing pattern as the "eight-ball" echo.
Finally, whatever happened to the z-components (cz and dz)? Because, by definition, these are perfectly aligned with the z-axis (and Bo field) they do not precess but remain locked in their vertical positions and are considered "stored". If a third RF-pulse were applied, cz and dz would have components tipped back into the transverse plane where they would again precess, rephase, and generate an echo. This is the origin of the stimulated echo (STE) discussed in the next Q&A.
Advanced Discussion (show/hide)»
Although I have stated a Hahn echo can be produced by any two pulses for simplicity of explanation, this is obviously not necessarily the case, in that the first pulse cannot be a multiple of 180 degrees.
References
Gallichan D. Some animations showing echo formation in MRI. Matlab code available at this link.
Hahn EL. Spin echoes. Phys Rev 1950;80:580-594. (The original duly famous paper where Hahn describes spin echoes).
Hennig J. Echoes — how to generate, recognize, use or avoid them in MR-imaging sequences. Part I: Fundamental and not so fundamental properties of spin echoes. Concepts Magn Reson 1991; 3:125-143.
Gallichan D. Some animations showing echo formation in MRI. Matlab code available at this link.
Hahn EL. Spin echoes. Phys Rev 1950;80:580-594. (The original duly famous paper where Hahn describes spin echoes).
Hennig J. Echoes — how to generate, recognize, use or avoid them in MR-imaging sequences. Part I: Fundamental and not so fundamental properties of spin echoes. Concepts Magn Reson 1991; 3:125-143.