|
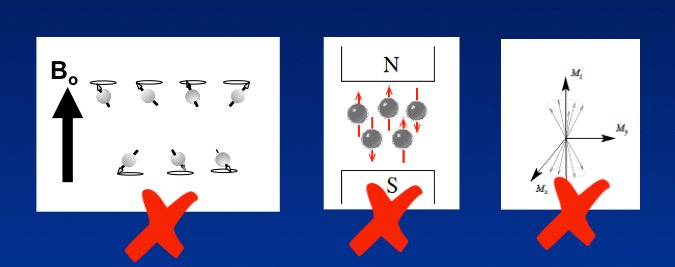
These diagrams and explanations, which have long pervaded nearly all of the popular literature on MRI, are both incomplete and misleading, as they are based on a superficial interpretation of quantum mechanical principles.
|
I felt like the proverbial "lone voice in the wilderness" as I began to point out these interpretative problems in the early 1990's in my lectures as visiting professor and in the first edition of Questions and Answers in Magnetic Resonance Imaging (1994). But few people seemed to be receptive or even listening. Perhaps MR physics was hard enough by itself without further muddying the waters by tossing in philosophical issues of quantum reality! In 2001 I was delighted to see British chemist Malcom Levitt try to set things straight in his textbook, Spin Dynamics, now in its second edition and definitely worth acquiring. More recently Danish physicist Lars Hanson has helped bring these and other quantum misconceptions further into light through his educational web site (http://www.drcmr.dk/MR). Hopefully others will follow suit.
Although it is perhaps easier to pretend these incorrect diagrams are "harmless", they nevertheless create their own set of problems for the serious thinker. If you are happy with these "conventional" explanations offered elsewhere, please skip to the next Q&A, because the following paragraphs will only serve to confuse you. But if the explanations offered in traditional sources haven't satisfied you, or if they have left you with more questions than answers, then read on.
Over the years, some of our brighter students have sought to go beyond these simplistic explanations offered in textbooks, drawing complex arrays of spin-up and spin-down protons precessing in various phase configurations in an attempt to model more detailed features of the NMR phenomenon. I admit that it is immensely appealing to try to construct such models; I did this myself early on and even now occasionally resort to drawing spinning tops for our students (while biting my tongue, of course!).
Although straightforward and comforting, these spinning top models depicting protons existing in only one of two orientations are fundamentally incorrect. No matter how complex one's arrays of spinning magnets become, the clever student will always be able to construct logical paradoxes exposing the models' inadequacies and inconsistencies. For example, if a proton can only point up or down, how do you make a 10° or 90° pulse? Why does the transverse magnetization immediately after a 90° pulse have exactly the same magnitude as the longitudinal magnetization immediately before the pulse? Why doesn't the RF field simply equalize the spin-up and spin-down populations? Why does continued application of the RF field cause the magnetization to rotate beyond 180° instead of simply forcing more and more protons into the spin-down state? And so on.
To answer these and similar questions, spin-up and spin-down top models simply will not suffice. To this end it will first be necessary to learn a little more about the true quantum mechanical description of a nuclear spin. Although this discussion is not usually presented in most radiology textbooks, we hope that our explanations will point the way to the "truth", even if they do not reveal it completely or to everyone's satisfaction. At a minimum, the reader should gain some insight into the way things work in the subatomic world. With this hope in mind, here goes:
Wave Function Formulation
The quantum mechanical description of a subatomic particle like the proton is based upon the premise of its wave-particle duality (i.e., that the proton simultaneously possesses properties of both a particle and a wave). This wave-like character is expressed in terms of the wave function, Ψ(t), which is a time-dependent solution to the Schrödinger equation describing the particle's energetics, with appropriate initial conditions and boundary constraints. In general, Ψ(t) contains a number of harmonically oscillating terms, separable into those affecting each of the particle's principal states. A hydrogen nucleus has two principal states, also known as eigenstates, denoted by the so-called "ket vectors" |+½⟩ and |−½⟩, and its wave function can be written
Although it is perhaps easier to pretend these incorrect diagrams are "harmless", they nevertheless create their own set of problems for the serious thinker. If you are happy with these "conventional" explanations offered elsewhere, please skip to the next Q&A, because the following paragraphs will only serve to confuse you. But if the explanations offered in traditional sources haven't satisfied you, or if they have left you with more questions than answers, then read on.
Over the years, some of our brighter students have sought to go beyond these simplistic explanations offered in textbooks, drawing complex arrays of spin-up and spin-down protons precessing in various phase configurations in an attempt to model more detailed features of the NMR phenomenon. I admit that it is immensely appealing to try to construct such models; I did this myself early on and even now occasionally resort to drawing spinning tops for our students (while biting my tongue, of course!).
Although straightforward and comforting, these spinning top models depicting protons existing in only one of two orientations are fundamentally incorrect. No matter how complex one's arrays of spinning magnets become, the clever student will always be able to construct logical paradoxes exposing the models' inadequacies and inconsistencies. For example, if a proton can only point up or down, how do you make a 10° or 90° pulse? Why does the transverse magnetization immediately after a 90° pulse have exactly the same magnitude as the longitudinal magnetization immediately before the pulse? Why doesn't the RF field simply equalize the spin-up and spin-down populations? Why does continued application of the RF field cause the magnetization to rotate beyond 180° instead of simply forcing more and more protons into the spin-down state? And so on.
To answer these and similar questions, spin-up and spin-down top models simply will not suffice. To this end it will first be necessary to learn a little more about the true quantum mechanical description of a nuclear spin. Although this discussion is not usually presented in most radiology textbooks, we hope that our explanations will point the way to the "truth", even if they do not reveal it completely or to everyone's satisfaction. At a minimum, the reader should gain some insight into the way things work in the subatomic world. With this hope in mind, here goes:
Wave Function Formulation
The quantum mechanical description of a subatomic particle like the proton is based upon the premise of its wave-particle duality (i.e., that the proton simultaneously possesses properties of both a particle and a wave). This wave-like character is expressed in terms of the wave function, Ψ(t), which is a time-dependent solution to the Schrödinger equation describing the particle's energetics, with appropriate initial conditions and boundary constraints. In general, Ψ(t) contains a number of harmonically oscillating terms, separable into those affecting each of the particle's principal states. A hydrogen nucleus has two principal states, also known as eigenstates, denoted by the so-called "ket vectors" |+½⟩ and |−½⟩, and its wave function can be written
Ψ(t) = a |+½⟩ + b |−½⟩
where a and b are time-dependent quantum amplitudes incorporating "harmonic oscillations" of each principal state. For a single proton placed in an external magnetic field, quantum analysis reveals that the terms a and b each contain a single harmonic frequency (½fo and −½fo, respectively), whose difference [½fo − (−½fo)] is the Larmor frequency fo = γ Bo.
Simple quantum mechanical descriptions of the NMR phenomena appearing in many books and websites imply that a spin can exist in either the spin-up or spin-down state exclusively and "flip" between them. These restrictions are not mandated in the wave function formulation and are actually misinterpretations of the wave function representation above. Quantum mechanics does not require that a spin reside exclusively in one or the other of its principal states; the only requirement is that the spin exist in some linear combination of the two states.
Simple quantum mechanical descriptions of the NMR phenomena appearing in many books and websites imply that a spin can exist in either the spin-up or spin-down state exclusively and "flip" between them. These restrictions are not mandated in the wave function formulation and are actually misinterpretations of the wave function representation above. Quantum mechanics does not require that a spin reside exclusively in one or the other of its principal states; the only requirement is that the spin exist in some linear combination of the two states.
|
Quantum "Reality"
The early fathers of quantum mechanics (Bohr, Heisenberg, Dirac, Schrödinger, and even Einstein) also struggled with the meaning of these eigenstates and the underlying "reality" they represented. We have already encountered one such problem in interpreting the Stern-Gerlach experiment where we saw that two discrete spots of silver atoms were deposited on a plate after passing through a strong magnetic field. Whenever we try to observe a spin physically (e.g., by measuring its energy or angular momentum), we always obtain a result referable to one of the two principal states, never an intermediate value. Does this mean the particle exists only in one of the pure states? The dominant answer to this question for the last century has been "No", elucidated by Bohr and Heisenberg and incorporated into what has become known as the Copenhagen Interpretation of quantum mechanics. Under this interpretation (as well as most others), the spin does not exist exclusively in one state or the other, but in a mixture of both states simultaneously. Whenever a physical measurement is made on the system, the wave function Ψ(t) somehow "collapses" and only a single state is observed in the macroscopic world. |
For a wave function with coefficients a and b, the probability of observing states |+½⟩ and |−½⟩ can be shown to be |a|² and |b|² respectively. The wave function Ψ(t) can therefore be thought of as a kind of probability distribution, expressing the likelihood that a given pure state will become revealed during a measuring experiment.
Although the issue is far from settled, recent experiments by Serge Haroche and David J. Wineland leading to their 2012 Nobel Prize in Physics may have put this matter to rest. Their results demonstrate that spins can simultaneously reside in two states simultaneously.
Working with different experimental setups, both Haroche and Wineland were able to trap photons and ions respectively in their superposition states, measuring and manipulating them in ways that were previously thought unattainable while preserving their quantum-mechanical nature. Haroche's and Wineland's work has allowed a better understanding of quantum superposition as well as the reasons why only a single state may be observed after a the measurement process.
Working with different experimental setups, both Haroche and Wineland were able to trap photons and ions respectively in their superposition states, measuring and manipulating them in ways that were previously thought unattainable while preserving their quantum-mechanical nature. Haroche's and Wineland's work has allowed a better understanding of quantum superposition as well as the reasons why only a single state may be observed after a the measurement process.
Although still the Copenhagen interpretation remains the most popular explanation of quantum reality, the Many Worlds Interpretation is gaining in popularity among physicists. In this model the proton also exists as a mixture of spin states prior to measurement, but instead of the wave function collapsing, the universe splits into two separate trajectories with each quantum decision. This fascinating approach to the universe is well beyond the scope of this web site, but the reader is encouraged to learn more about these ideas from the references below.
|
Of course, the answers are not all in. Quantum mechanics remains incomplete and there remain many unanswered questions and problems, especially concerning entanglement and mechanism of action at a distance.
Anyone with a spare hour to kill might enjoy the YouTube video right. |
|
Advanced Discussion (show/hide)»
No supplementary material yet. Check back soon.
References
Bergström L, Jonson B, Delsning P, l'Huillier A. Particle control in a quantum world. Royal Swedish Academy of Sciences. Nobel Prize in Physics, 2012, pp 1-6.
Copenhagen Interpretation. Wikipedia, The Free Encyclopedia.
Einstein A, Podolsky B, Rosen N. Can quantum-mechanical description of physical reality be considered complete? Phys Rev 1935;47:777-780 (Slightly off topic, but a widely quoted paper proposing the famous EPR paradox. All serious philosophers of science know about this).
Elster AD. Questions and Answers in MRI, 1st Ed. St. Louis: Mobsy, 1994, pp. 26-28.
Hanson L. Is quantum mechanics necessary for understanding magnetic resonance? Concepts Mag Reson Part A 2008;32A(5):329-340.
Levitt MH. Spin Dynamics. Basis of Nuclear Magnetic Resonance, 2nd Ed. Chichester, UK: Wiley, 2011.
Mompart J. The Gedankenexperimente of quantum mechanics become reality: on the 2012 Nobel Prize in physics, awarded to Serge Haroche and David J. Wineland. Contrib Sci 2013; 9:33-41.
Raimond JM, Brune M, Haroche S. Colloquium: Manipulating quantum entanglement with atoms and photons in a cavity. Rev Mod Phys 2001; 73: 565-582
Zurek WH. Decoherence, einselection, and the quantum origins of the classical. Rev Mod Phys 2003; 75:716-775.
Bergström L, Jonson B, Delsning P, l'Huillier A. Particle control in a quantum world. Royal Swedish Academy of Sciences. Nobel Prize in Physics, 2012, pp 1-6.
Copenhagen Interpretation. Wikipedia, The Free Encyclopedia.
Einstein A, Podolsky B, Rosen N. Can quantum-mechanical description of physical reality be considered complete? Phys Rev 1935;47:777-780 (Slightly off topic, but a widely quoted paper proposing the famous EPR paradox. All serious philosophers of science know about this).
Elster AD. Questions and Answers in MRI, 1st Ed. St. Louis: Mobsy, 1994, pp. 26-28.
Hanson L. Is quantum mechanics necessary for understanding magnetic resonance? Concepts Mag Reson Part A 2008;32A(5):329-340.
Levitt MH. Spin Dynamics. Basis of Nuclear Magnetic Resonance, 2nd Ed. Chichester, UK: Wiley, 2011.
Mompart J. The Gedankenexperimente of quantum mechanics become reality: on the 2012 Nobel Prize in physics, awarded to Serge Haroche and David J. Wineland. Contrib Sci 2013; 9:33-41.
Raimond JM, Brune M, Haroche S. Colloquium: Manipulating quantum entanglement with atoms and photons in a cavity. Rev Mod Phys 2001; 73: 565-582
Zurek WH. Decoherence, einselection, and the quantum origins of the classical. Rev Mod Phys 2003; 75:716-775.
Related Questions
What is the difference between "spin" and "spin state"?
What is the difference between "spin" and "spin state"?