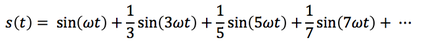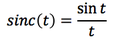|
The Fourier transform is a mathematical technique that allows an MR signal to be decomposed into a sum of sine waves of different frequencies, phases, and amplitudes. This remarkable result derives from the work of Jean-Baptiste Joseph Fourier (1768-1830), a French mathematician and physicist. Since spatial encoding in MR imaging involves frequencies and phases, it is naturally amenable to analysis by Fourier techniques.
Fourier showed that any periodic signal s(t) can be written as a sum of sine waves with various amplitudies, frequencies and phases
|
|
Fourier transformation is the mathematical procedure connecting s(t) and S(ω). If s(t) is specified, S(ω) may be computed, and vice versa. The equations require some knowledge of complex numbers and calculus to make sense, but don't worry if you don't understand them. There is some supplemental material in the Advanced Discussion section for interested readers. Here I will simply provide the defining equations for completeness:
|
|
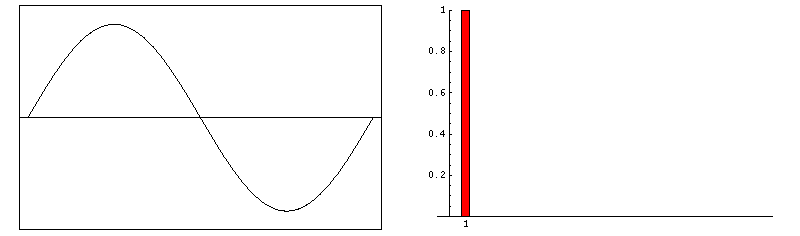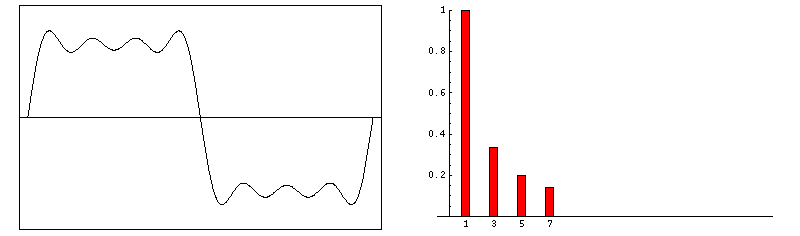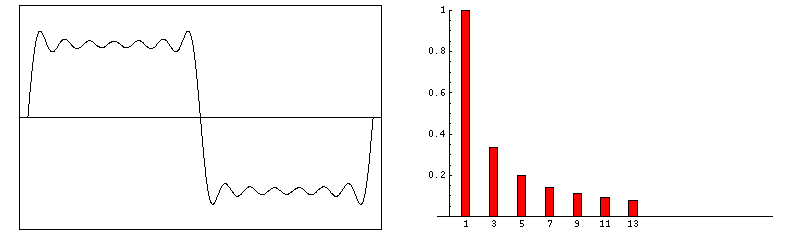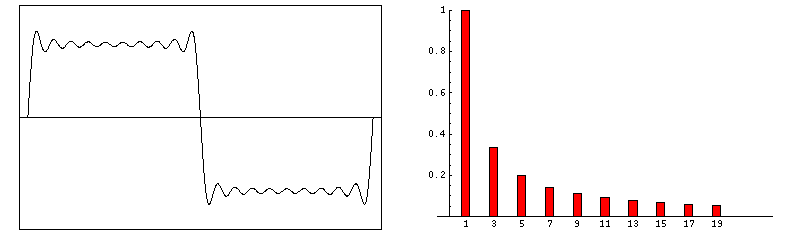
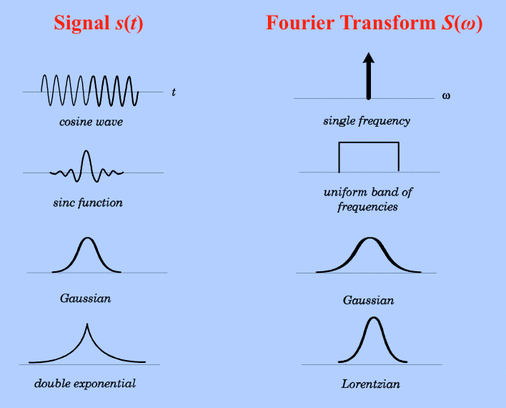
Because it is not immediately obvious what S(ω) looks like for a given s(t), I have drawn a several Fourier transform pairs for comparison. Note that when s(t) is spread out in time, S(ω) is compact, and vice-versa. One entry that deserves special notice because of its common use in RF-pulse design is the sinc function
whose Fourier transform is a uniform band of frequencies, such as those defining a single slice in conventional 2D MR imaging.
|
Advanced Discussion (show/hide)»
A few additional notes about Fourier transforms...
1. The equations given for the Fourier and inverse Fourier transforms are often written slightly differently in mathematical, engineering, and physics texts. Sometimes the 1/2π term is associated with the forward transform is shared equally in square root form between the two equations. The minus sign in the exponent for e is sometimes switched between the two forms. Engineers often use the letter "j" instead of "i" for the imaginary unit, so as not to cause confusion with the symbol for electrical current.
2. To represent any real signal exactly, an infinite number of frequency components must be included in its Fourier representation. Clearly this condition cannot be met in MR imaging, since our computer memory is limited and a finite digitizing rate permits us to sample only a limited band of frequencies contained within the actual signal. The Fourier series representation of an MR image must therefore be cut short (truncated) at some point, giving rise to characteristic errors in its reconstruction. These "truncation" or "Gibbs" artifacts are the subject of a later Q&A.
3. The graphical representation of the Fourier transform as a set of frequencies and amplitudes is only part of the picture. For simplicity of explanation I have left out the fact that phase shifts (ϕi) corresponding to each frequency must also be included. This is where the use of imaginary numbers and the theory of complex variable calculus comes in. The Euler notation is commonly used in the definition of the Fourier transform: eiωt = cos(ωt) + i sin(ωt), where i2 = −1, the imaginary unit. This results in S(ω) having both a real and imaginary components, Re(ω) and Im(ω), where the Im(ω) terms are all multiplied by i. In other words, S(ω) = Re(ω) + i Im(ω). The associated phase shift Φ(ω) for a given frequency is therefore
Φ(ω) = arctan [Im(ω)/Re(ω)]
In ¹H NMR magnetization precesses counterclockwise when viewed from above (i.e., from the the +x-axis toward the −y-axis). By convention, this means that the angular frequency (ω) is negative. The Euler expression is often written e−iωt = cos(−ωt) + i sin(−ωt) = cos(ωt) − i sin(ωt) based on the identities cos(−x)= cos(x) and sin(−x) = −sin(x).
Bracewell R. The Fourier transform and its applications, 2nd ed. New York: McGraw-Hill, 1986. (This classic textbook requires a knowledge of calculus, but has numerous line drawings and explanations as well. Nearly all the physicists and engineers of my generation I know who work in MR own or have read this book.)
Cooley JW, Tukey JW. An algorithm for the machine calculation of complex Fourier series. Math Comput 1965; 19:297-301. (The famous Fast Fourier Transform (FFT) algorithm, some variant of which is used in all MR systems for image processing).
Gallagher TA, Nemeth AJ, Hacein-Bey L. An introduction to the Fourier transform: relationship to MRI. AJR Am J Roentgenol 2008; 190:1396-1405.
"Joseph Fourier". Wikipedia, the Free Encyclopedia. (A fascinating life and history. Fourier travelled with Napoleon to Egypt and was nearly executed by Robespierre. He also is credited with discovering the "greenhouse effect.")
Russell DA. Acoustics and vibration animations. (A wonderful web site with great animations of various interacting waves from the Graduate Program in Acoustics at Penn State).
How does the scanner know the locations of all the MR signals?
How does frequency-encoding work?