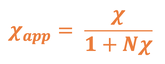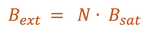|
Moderately to strongly ferromagnetic materials
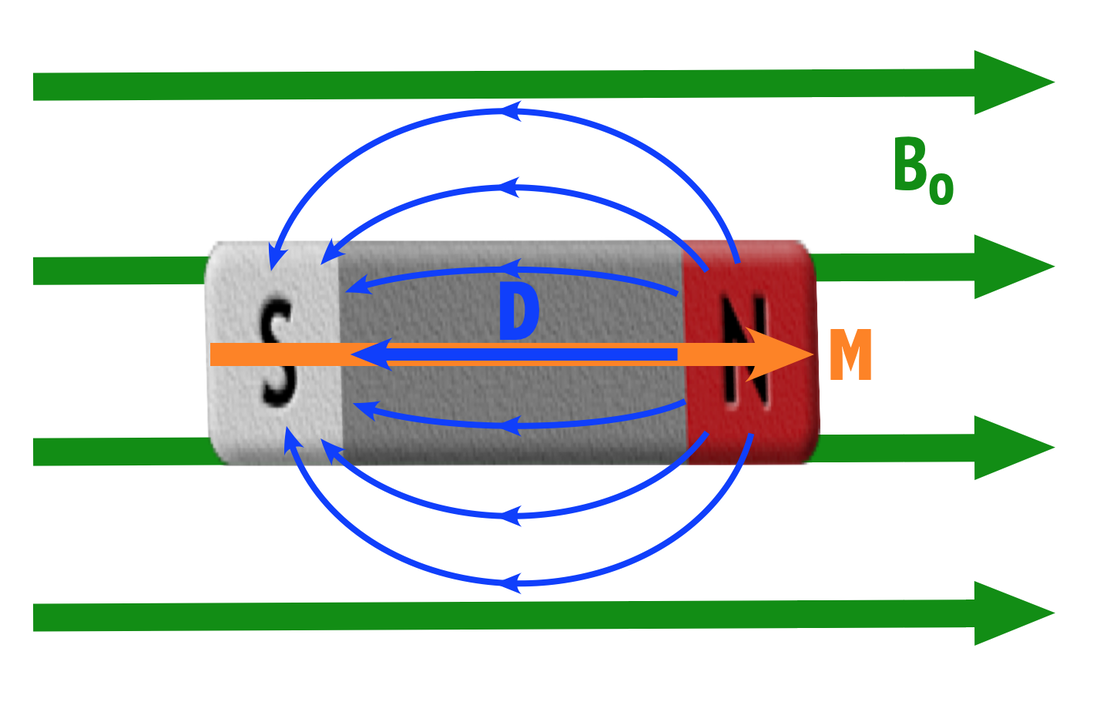
Objects made of iron, nickel, and/or chromium with larger susceptibilities (χ >> 1) become progressively magnetized when placed in an external magnetic field (Bo). As the external field increases, so does this internal polarization/ magnetization (M) as electron spins begin to align and magnetic domain boundaries are reshaped. This process continues until M reaches the magnetic saturation point of the material, beyond which no further magnetization can occur. (Note that the magnetic polarization M arises from electron spins in microscopic currents and has nothing to do with nuclear magnetization M discussed elsewhere).
|
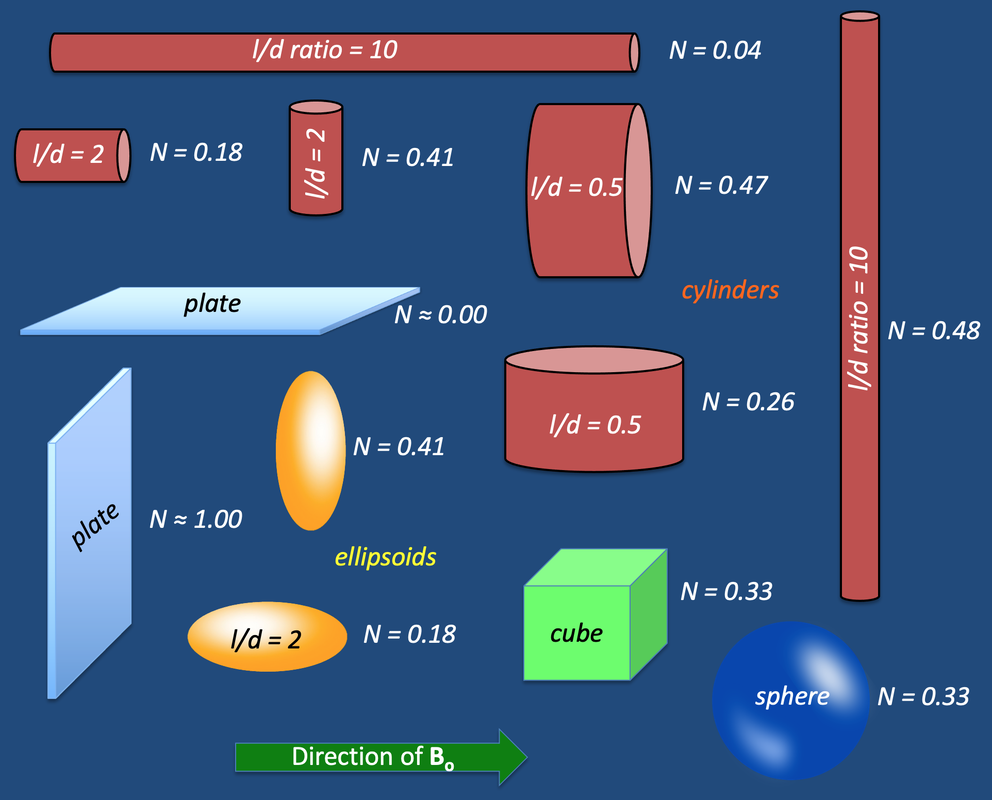
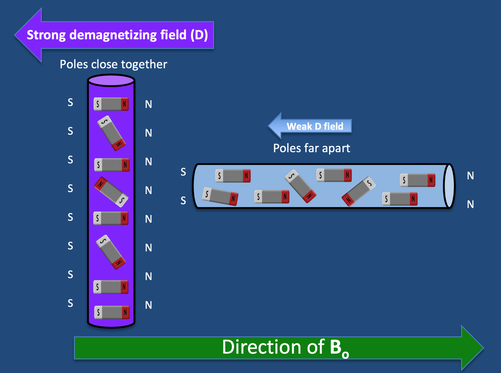
Note that objects with the highest N-values are those that have a large relative surface area facing in the direction of Bo. Such an object is typified by the thin vertical plate perpendicular to Bo, which has N ≈ 1.00 (the highest possible value). Conversely, when the plate is turned by 90º, N ≈ 0.00 (the lowest possible value). The same principle is demonstrated by the various ellipsoids and cylinders illustrated.
Advanced Discussion (show/hide)»
By definition, the magnetization M is related to the internal magnetic field (H) through the dimensionless quantity (χ) known as the magnetic susceptibility:
M = χ H
In diagmagnetic and weakly paramagnetic materials, H = Ho, where Ho is the external field.
In ferromagnetic materials shape plays a critical role because the internal field H is reduced by an opposing demagnetizing field (D), which for homogeneous linear materials can be written as D = − NM, where N is a direction specific demagnetizing factor.
So in ferromagnetic materials
H = Ho − D = Ho − NM
But since H = M / χ we can write
M / χ = Ho − NM
or
Ho = M / χ + NM = M
The apparent susceptibility χapp is therefore
χapp = M / Ho = χ /
Dividing the numerator and denominator by χ we obtain
χapp = 1 /
So when χ → ∞, 1/χ → 0, and we are left with
χapp = 1 / N
Thus for large values of χ (as are typically found in ferromagnetic materials), the dependence on χ disappears, with the apparent susceptibility dependent only on the reciprocal (1/N) of the demagnetizing factor.
The strength of the external field (Hext) needed to cause magnetic saturation (Msat) can be derived as
Hext = Msat / χapp = Msat / (1/N) = NMsat
Converting to SI units by multiplying each side of this equation by the permeability of free space (μo = 4π x 10−7 T m A−1), with Bext = μoHext and Bsat = μoMsat we obtain
Bext = N Bsat
Jackson DP. Dancing paperclips and the geometric influence on magnetization: a surprising result. Am J Phys 2006; 74:272-279.
McRobbie DW. Essentials of MRI Safety. Wiley-Blackwell, 2020. (Excellent recently released book. Chapter 2 on Fields and Forces as well as Appendix is very pertinent to this topic). [Link to purchase]
Osborn JA. Demagnetizing factors of the general ellipsoid. Phys Rev 1945; 67:351-357. [DOI link]
Panych LP, Kimbrell VK, Mukundan Jr S, Madore B. Relative magnetic force measures and their potential role in MRI safety practice. J Magn Reson Imaging 2020; 51:1260-1271. [DOI Link]
Prozorov R, Kogan VG. Effective demagnetizing factors of diamagnetic samples of various shapes. arXiv:1712.06037v2 (2 July 2018)
Sato M, Ishii Y. Simple and approximate expressions of demagnetizing factors of uniformly magnetized rectangular rod and cylinder. J App Phys 1989; 66:983-5. [DOI Link]
Skomski R, Hadjipanayis GC, Sellmyer DJ. Effective demagnetizing factors of complicated particle mixtures. IEEE Trans Magnetics 2007; 43:2956-8. [DOI Link]
Snelling EC. Soft Ferrites. Properties and Applications. Iliffe Books:London, 1969: selected pages
Solivérez CE. Electrostatics and magnetostatics of polarized ellipsoidal bodies: The depolarization tensor method. Bariloche: Rio Negro, Argentina: 2016.
Wysin GM. Demagnetization fields. 2012:1-16. Public teaching notes, downloaded from this link, 20 Oct 2020.
Which types of metal are the most dangerous around a magnetic field?
What is magnetic susceptibility?
What is ferromagnetism?